Parallel and multithreaded functions

Questions

• What is parallel programming?

• Why do we need it?

• When can I use it?

Objectives

• Learn basic concepts in parallel programming

• Gain knowledge on the tools for parallel programming in different languages

• Familiarize with the tools to monitor the usage of resources

What is parallel programming?

Parallel programming is the science and art of writing code that execute tasks on different computing units (cores) simultaneously. In the past computers were shiped with a single core per Central Processing Unit (CPU) and therefore only a single computation at the time (serial program) could be executed.

Nowadays computer architectures are more complex than the single core CPU mentioned already. For instance, common architectures include those where several cores in a CPU share a common memory space and also those where CPUs are connected through some network interconnect.

Shared Memory and Distributed Memory architectures.

A more realistic picture of a computer architecture can be seen in the following picture where we have 14 cores that shared a common memory of 64 GB. These cores form the socket and the two sockets shown in this picture constitute a node.

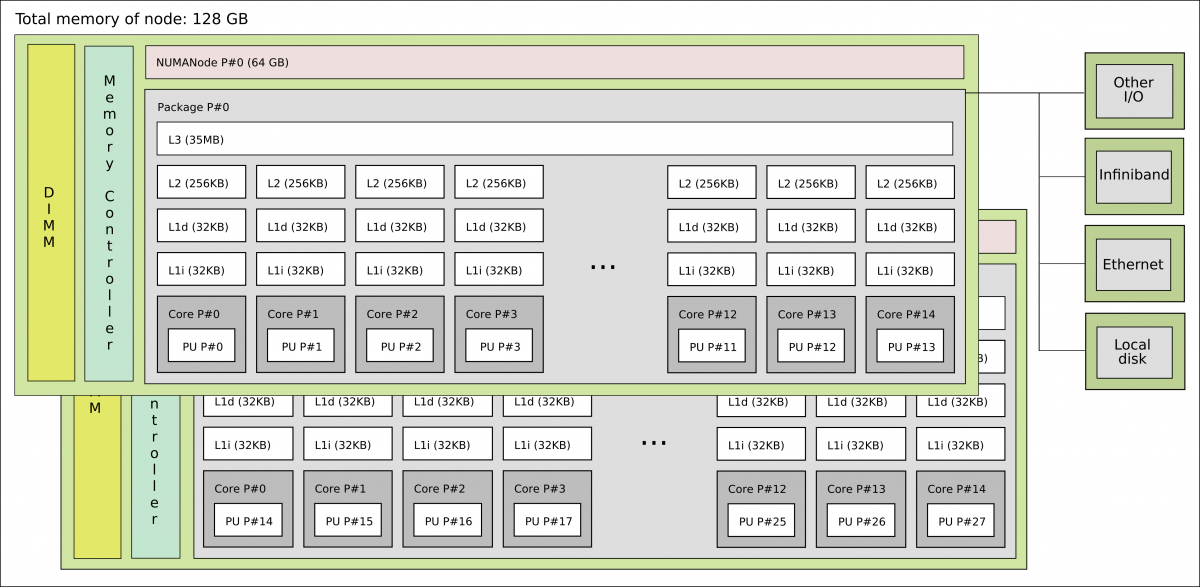
1 standard node on Kebnekaise @HPC2N

It is interesting to notice that there are different types of memory available for the cores, ranging from the L1 cache to the node’s memory for a single node. In the former, the bandwidth can be TB/s while in the latter GB/s.

Now you can see that on a single node you already have several computing units (cores) and also a hierarchy of memory resources which is denoted as Non Uniform Memory Access (NUMA).

Besides the standard CPUs, nowadays one finds Graphic Processing Units (GPUs) architectures in HPC clusters.

Why is parallel programming needed?

There is no “free lunch” when trying to use features (computing/memory resources) in modern architectures. If you want your code to be aware of those features, you will need to either add them explicitly (by coding them yourself) or implicitly (by using libraries that were coded by others).

In your local machine, you may have some number of cores available and some memory attached to them which can be exploited by using a parallel program. There can be some limited resources for running your data-production simulations as you may use your local machine for other purposes such as writing a manuscript, making a presentation, etc. One alternative to your local machine can be a High Performance Computing (HPC) cluster another could be a cloud service. A common layout for the resources in an HPC cluster is a shown in the figure below.

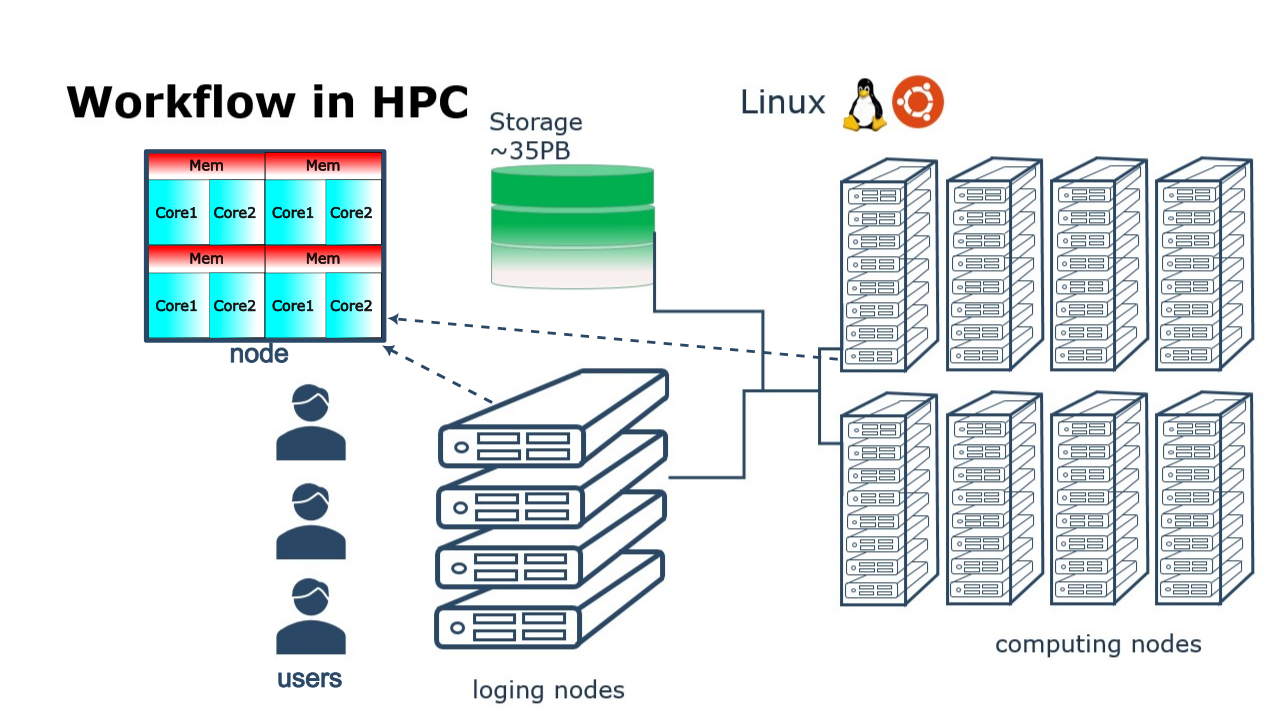
High Performance Computing (HPC) cluster.

Although a serial application can run in such a cluster, it would not gain much of the HPC resources. If fact, one can underuse the cluster if one allocates more resources than what the simulation requires.

Under-using a cluster.

Warning

• Check if the resources that you allocated are being used properly.

• Monitor the usage of hardware resources with tools offered at your HPC center, for instance job-usage at HPC2N.

• Here there are some examples (of many) of what you will need to pay attention when porting a parallel code from your laptop (or another HPC center) to our clusters:

HPC2NUPPMAX

We have a tool to monitor the usage of resources called: job-usage at HPC2N.

Common parallel programming paradigms

Now the question is how to take advantage of modern architectures which consist of many-cores, interconnected through networks, and that have different types of memory available? Python, Julia, Matlab, and R languages have different tools and libraries that can help you to get more from your local machine or HPC cluster resources.

Threaded programming

To take advantage of the shared memory of the cores, threaded mechanisms can be used. Low-level programming languages, such as Fortran/C/C++, use OpenMP as the standard application programming interface (API) to parallelize programs by using a threaded mechanism. Here, all threads have access to the same data and can do computations simultaneously. From this we infer that without doing any modification to our code we can get the benefits from parallel computing by turning-on/off external libraries, by setting environment variables such as OMP_NUM_THREADS.

Higher-level languages have their own mechanisms to generate threads and this can be confusing especially if the code is using external libraries, linear algebra for instance (LAPACK, BLAS, …). These libraries have their own threads (OpenMP for example) and the code you are writing (R, Julia, Python, or Matlab) can also have some internal threded mechanism.

Warning

• Check if the libraries/packages that you are using have a threaded mechanism.

• Monitor the usage of hardware resources with tools offered at your HPC center, for instance job-usage at HPC2N.

• Here there are some examples (of many) of what you will need to pay attention when porting a parallel code from your laptop (or another HPC center) to our clusters:

PythonJuliaRMatlab

For some linear algebra operations Numpy supports threads (set with the OMP_NUM_THREADS variable). If your code contains calls to these operations in a loop that is already parallelized by n processes, and you allocate n cores for this job, this job will exceed the allocated resources unless the number of threads is explicitly set to 1.

A common issue with shared memory programming is data racing which happens when different threads write on the same memory address.

Language-specific nuances for threaded programming

PythonJuliaRMatlab

Python offers its own threaded mechanism but due to a locking mechanism, Python threads are not efficient for computation. However, Python threads could be useful for I/O files handling. Code modifications are required to support the threads.

Distributed programming

Although threaded programming is convenient because one can achieve considerable initial speedups with little code modifications, this approach does not scale for more than hundreds of cores. Scalability can be achieved with distributed programming. Here, there is not a common shared memory but the individual processes (notice the different terminology with threads in shared memory) have their own memory space. Then, if a process requires data from or should transfer data to another process, it can do that by using send and receive to transfer messages. A standard API for distributed computing is the Message Passing Interface (MPI). In general, MPI requires refactoring of your code.

Language-specific nuances for distributed programming

PythonJuliaRMatlab

Python has different modules for achieving distributed programming, for instance multiprocessing and mpi4py. The former is part of the Python standard library so you don’t need to do further installations, while the latter needs to be installed. Also, one needs to learn the concepts of MPI prior to using the feautures offered by this module.

Big data

Sometimes the workflow you are targeting doesn’t require extensive computations but mainly dealing with big pieces of data. An example can be, reading a column-structured file and doing some transformation per-column. Fortunately, all languages covered in this course have already several tools to deal with big data. We list some of these tools in what follows but notice that other tools doing similar jobs can be available for each language.

Language-specific tools for big data

PythonJuliaRMatlab

Dask

Dask is a array model extension and task scheduler. By using the new array classes, you can automatically distribute operations across multiple CPUs.

Dask is very popular for data analysis and is used by a number of high-level Python libraries:

• Dask arrays scale NumPy (see also xarray)

• Dask dataframes scale Pandas workflows

• Dask-ML scales Scikit-Learn

• Dask divides arrays into many small pieces (chunks), as small as necessary to fit it into memory.

• Operations are delayed (lazy computing) e.g. tasks are queue and no computation is performed until you actually ask values to be computed (for instance print mean values).

• Then data is loaded into memory and computation proceeds in a streaming fashion, block-by-block.

• An example of a Jupyter notebook running Dask can be found here.

---

Demo

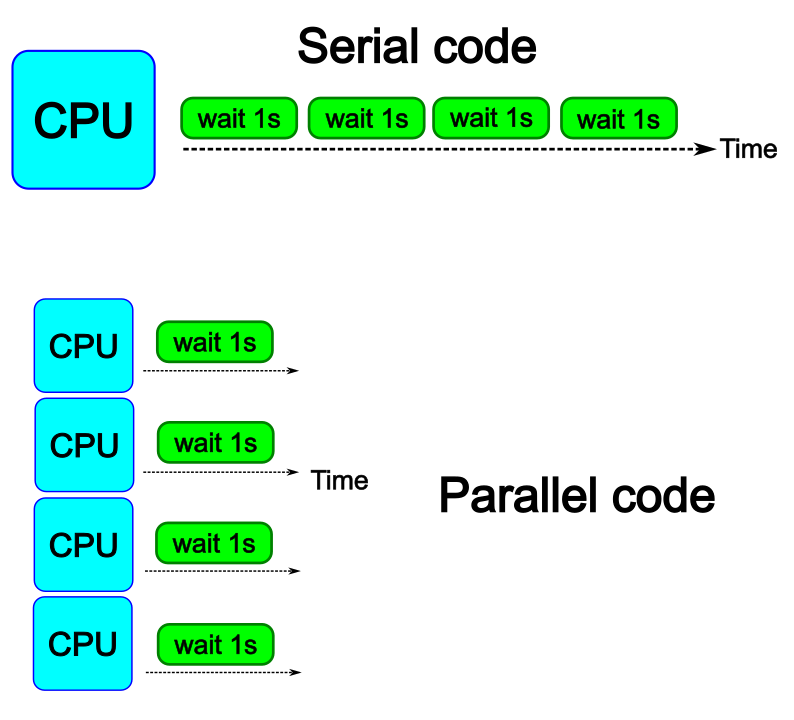
The idea is to parallelize a simple for loop (language-agnostic):

for i start at 1 end at 4
   wait 1 second
end the for loop

The waiting step is used to simulate a task without writing too much code. In this way, one can realize how faster the loop can be executed when threads are added:

PythonJuliaRMatlab

In the following example sleep.py the sleep() function is called n times first in serial mode and then by using n processes. To parallelize the serial code we can use the multiprocessing module that is shipped with the base library in Python so that you don’t need to install it.

import sys
from time import perf_counter,sleep
import multiprocessing

# number of iterations
n = 4
# number of processes
numprocesses = 4

def sleep_serial(n):
    for i in range(n):
        sleep(1)


def sleep_threaded(n,numprocesses,processindex):
    # workload for each process
    workload = n/numprocesses
    begin = int(workload*processindex)
    end = int(workload*(processindex+1))
    for i in range(begin,end):
        sleep(1)

if __name__ == "__main__":

    starttime = perf_counter()   # Start timing serial code
    sleep_serial(n)
    endtime = perf_counter()

    print("Time spent serial: %.2f sec" % (endtime-starttime))


    starttime = perf_counter()   # Start timing parallel code
    processes = []
    for i in range(numprocesses):
        p = multiprocessing.Process(target=sleep_threaded, args=(n,numprocesses,i))
        processes.append(p)
        p.start()

    # waiting for the processes
    for p in processes:
        p.join()

    endtime = perf_counter()

    print("Time spent parallel: %.2f sec" % (endtime-starttime))

First load the modules ml GCCcore/11.2.0 Python/3.9.6 and then run the script with the command srun -A "your-project" -n 1 -c 4 -t 00:05:00 python sleep.py to use 4 processes.

---

Exercises

Running a parallel code efficiently

In this exercise we will run a parallelized code that performs a 2D integration:

\[\int^{\pi}_{0}\int^{\pi}_{0}\sin(x+y)dxdy = 0\]

One way to perform the integration is by creating a grid in the x and y directions. More specifically, one divides the integration range in both directions into n bins.

PythonJuliaRMatlab

Here is a parallel code using the multiprocessing module in Python (call it integration2d_multiprocessing.py):

integration2d_multiprocessing.py

import multiprocessing
from multiprocessing import Array
import math
import sys
from time import perf_counter

# grid size
n = 5000
# number of processes
numprocesses = *FIXME*
# partial sum for each thread
partial_integrals = Array('d',[0]*numprocesses, lock=False)

# Implementation of the 2D integration function (non-optimal implementation)
def integration2d_multiprocessing(n,numprocesses,processindex):
   global partial_integrals;
   # interval size (same for X and Y)
   h = math.pi / float(n)
   # cummulative variable
   mysum = 0.0
   # workload for each process
   workload = n/numprocesses

   begin = int(workload*processindex)
   end = int(workload*(processindex+1))
   # regular integration in the X axis
   for i in range(begin,end):
      x = h * (i + 0.5)
      # regular integration in the Y axis
      for j in range(n):
            y = h * (j + 0.5)
            mysum += math.sin(x + y)

   partial_integrals[processindex] = h**2 * mysum


if __name__ == "__main__":

   starttime = perf_counter()

   processes = []
   for i in range(numprocesses):
      p = multiprocessing.Process(target=integration2d_multiprocessing, args=(n,numprocesses,i))
      processes.append(p)
      p.start()

   # waiting for the processes
   for p in processes:
      p.join()

   integral = sum(partial_integrals)
   endtime = perf_counter()

print("Integral value is %e, Error is %e" % (integral, abs(integral - 0.0)))
print("Time spent: %.2f sec" % (endtime-starttime))

Run the code with the following batch script.

job.sh

UPPMAXHPC2NLUNARC

#!/bin/bash -l
#SBATCH -A naiss202X-XY-XYZ     # your project_ID
#SBATCH -J job-serial           # name of the job
#SBATCH -n *FIXME*              # nr. tasks/coresw
#SBATCH --time=00:20:00         # requested time
#SBATCH --error=job.%J.err      # error file
#SBATCH --output=job.%J.out     # output file

# Load any modules you need, here for Python 3.11.8 and compatible SciPy-bundle
module load python/3.11.8
python integration2d_multiprocessing.py

Try different number of cores for this batch script (FIXME string) using the sequence: 1,2,4,8,12, and 14. Note: this number should match the number of processes (also a FIXME string) in the Python script. Collect the timings that are printed out in the job.*.out. According to these execution times what would be the number of cores that gives the optimal (fastest) simulation?

Challenge: Increase the grid size (n) to 15000 and submit the batch job with 4 workers (in the Python script) and request 5 cores in the batch script. Monitor the usage of resources with tools available at your center, for instance top (UPPMAX) or job-usage (HPC2N).

Parallelizing a for loop workflow (Advanced)

Create a Data Frame containing two features, one called ID which has integer values from 1 to 10000, and the other called Value that contains 10000 integers starting from 3 and goes in steps of 2 (3, 5, 7, …). The following codes contain parallelized workflows whose goal is to compute the average of the whole feature Value using some number of workers. Substitute the FIXME strings in the following codes to perform the tasks given in the comments.

The main idea for all languages is to divide the workload across all workers. You can run the codes as suggested for each language.

PythonJuliaRMatlab

Pandas is available in the following combo ml GCC/12.3.0 SciPy-bundle/2023.07 (HPC2N) and ml python/3.11.8 (UPPMAX). Call the script script-df.py.

import pandas as pd
import multiprocessing

# Create a DataFrame with two sets of values ID and Value
data_df = pd.DataFrame({
    'ID': range(1, 10001),
    'Value': range(3, 20002, 2)  # Generate 10000 odd numbers starting from 3
})

# Define a function to calculate the sum of a vector
def calculate_sum(values):
    total_sum = *FIXME*(values)
    return *FIXME*

# Split the 'Value' column into chunks of size 1000
chunk_size = *FIXME*
value_chunks = [data_df['Value'][*FIXME*:*FIXME*] for i in range(0, len(data_df['*FIXME*']), *FIXME*)]

# Create a Pool of 4 worker processes, this is required by multiprocessing
pool = multiprocessing.Pool(processes=*FIXME*)

# Map the calculate_sum function to each chunk of data in parallel
results = pool.map(*FIXME: function*, *FIXME: chunk size*)

# Close the pool to free up resources, if the pool won't be used further
pool.close()

# Combine the partial results to get the total sum
total_sum = sum(results)

# Compute the mean by dividing the total sum by the total length of the column 'Value'
mean_value = *FIXME* / len(data_df['*FIXME*'])

# Print the mean value
print(mean_value)

Run the code with the batch script:

UPPMAXHPC2NLUNARC

#!/bin/bash -l
#SBATCH -A naiss2024-22-107  # your project_ID
#SBATCH -J job-parallel      # name of the job
#SBATCH -n 4                 # nr. tasks/coresw
#SBATCH --time=00:20:00      # requested time
#SBATCH --error=job.%J.err   # error file
#SBATCH --output=job.%J.out  # output file

# Load any modules you need, here for Python 3.11.8 and compatible SciPy-bundle
module load python/3.11.8
python script-df.py

Solution

PythonJuliaRMatlab

import pandas as pd
import multiprocessing

# Create a DataFrame with two sets of values ID and Value
data_df = pd.DataFrame({
    'ID': range(1, 10001),
    'Value': range(3, 20002, 2)  # Generate 10000 odd numbers starting from 3
})

# Define a function to calculate the sum of a vector
def calculate_sum(values):
    total_sum = sum(values)
    return total_sum

# Split the 'Value' column into chunks
chunk_size = 1000
value_chunks = [data_df['Value'][i:i+chunk_size] for i in range(0, len(data_df['Value']), chunk_size)]

# Create a Pool of 4 worker processes, this is required by multiprocessing
pool = multiprocessing.Pool(processes=4)

# Map the calculate_sum function to each chunk of data in parallel
results = pool.map(calculate_sum, value_chunks)

# Close the pool to free up resources, if the pool won't be used further
pool.close()

# Combine the partial results to get the total sum
total_sum = sum(results)

# Compute the mean by dividing the total sum by the total length of the column 'Value'
mean_value = total_sum / len(data_df['Value'])

# Print the mean value
print(mean_value)

More info

• HPC2N Julia documentation.

• White paper on Julia parallel computing.

• HPC2N R documentation.

• Introduction to Dask by Aalto Scientific Computing and CodeRefinery

• Intermediate level Dask by ENCCS.

• Official Python documentation.

• Wikipedias’ article on Parallel Computing

• The book High Performance Python is a good resource for ways of speeding up Python code.